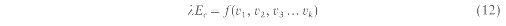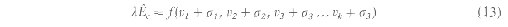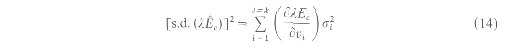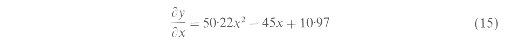| Res14 |

|
 |  | ||||
| |||||
S. N. V. KALLURI, J. R. G. TOWNSHEND and P. DORAISWAMY (Received 26 July 1990; in final form 14 July 1997) ABSTRACTA methodology is developed here to model evapotranspiration (lEc) from the canory laver over large areas by combining satellite and ground measurements of biophysical and meteorological variables. The model developed here follows the energy balance approach, where lEc is estimated as a residual when the net radiation (Rn), sensible heat flux (H) and ground flux (G) are known. Multi-spectral measurements from the NOAA Advanced Very High Resolution Radiometer (AVHRR) were used along with routine meteorological measurements made on the ground to estimate components of the energy balance. The upwelling long wave radiation, and H from the canopy layer were modelled using the canopy temperature, obtained from a linear relation between the Normalized Difference Vegetation Index (NDVI) and surface temperature. This method separates flux measurements from the canopy and bare soil without the need for a complex two layer model. From theoretical analysis of canopy reflectance, leaf area, and canopy resistance, a model is developed to scale the transpiration estimates from the full canopy to give an area averaged estimate from the mean NDVI of the study area. The model was tested using data collected from the First International Satellite Land Surface Climatology Project (ISLSCP) Field Experiment (FIFE), and the results show that the modelled values of total surface evapotranspiration from the soil and canopy layers vary from the ground measurements by less than 9 per cent. INTRODUCTIONEstimating evapotranspiration (lE) is important in studies related to land surface energy balance and climatology. Remotely-sensed multi-spectral measurements are widely used to determine the variables required to model lE (for example, Jackson 1985. Seguin and Itier 1983, Choudhury 1989, Kustas et at. 1990, Price 1990), since remote sensing can provide us with synoptic multi-temporal measurements over larger areas. Although most of the spaceborric remote sensing platforms provide us with instantaneous measurements of the land surface variables, previous studies have shown that daily estimates of lE can be made from instantaneous measurements (e.g., Jackson 1985, Kustas et al. 1990). lE consists of evaporation and transpiration from the vegetation layer (lEc) and evaporation from the background soil layer (lEsoil). Over vegetated areas, lEc, is the dominant component in lE. The intake of atmospheric carbon dioxide by the plants for photosynthesis is proportional to the water transpired, since the diffusion of carbon dioxide and water vapour between the atmosphere and the plant occur simultaneously through the plants stomates (Cowan 1982, Nobel 1983), and several studies have related crop yields to lE (de Wit 1958, Tanner 1981, and Tanner and Sinclair 1983). The ratio of actual evapotranspiration (lE) and potential evapotranspiration (lPE) has been widely used to quantify water stress in vegetation (Jackson et tit. 1981, O'Toole ci (it. 1984). Thus. information regarding the spatial and temporal variability of transpiration will help us monitor crop water requirements, and the degree and duration of water shortage in plants.The surface energy balance is written as:
where Rn is the net radiation, G is soil heat flux. H is the sensible heat flux, and lE is the amount of water evaporated and transpired per unit area during the process of latent heat (LE) exchange between the canopy and the atmosphere. When expressed in energy units, the fluxes of LE and lE are identical. Rn is the net balance of the incoming and outgoing radiative fluxes at the surface, and can be written as:
where SW is the shortwave radiation, a is the surface albedo, and LIV is the longwave radiation. All the components of the energy balance Rn G, H, T, SW and LIV are expressed in W m-2. The up and down arrows indicate the direction of fluxes away and towards the surface respectively. The total daily magnitude of G is negligible over vegetation areas (Choudhury 1994). H and lEc can be parameterized as:
where rcp is the volumetric heat capacity of the air (~1200 J m3 K-1), T0 and Ta, are the surface and air temperatures (deg K) respectively, and ra is the aerodynamic resistance of the surface (s m-1). ra is determined from wind speed and surface roughness. H is dependent upon the magnitude of ra, and the difference between the surface and air temperatures.
In (4) e's is the saturated vapour pressure (kPa) at T0, ea is the actual vapour pressure (kPa) at Ta, g is the psychrometric constant (~0.066 kPa K-1), ra is the canopy resistance (s m-1), and rs is the reciprocal of canopy conductance (gc). The partitioning of the absorbed solar energy between H and lEc depends on the availability of water to the plant. Under conditions where the water supply is not limited, and where there is full canopy cover most of the energy is partitioned towards lEc, otherwise energy is partitioned towards H. Inadequate water supply decreases the evaporative heat loss from the plants due to stomatal closure resulting in an increase in canopy temperature, leading to an increase in H (Campbell and Norman 1990). In heterogeneous areas where the land cover is a mixture of bare soil and vegetation (which is usually the case), two energy budget equations are needed, one for the vegetation and another for bare soil. Since the sensible and latent heat fluxes are not a linear function of surface variables, such as temperature and resistance, spatially averaged parameters inay not provide a correct estimate of these fluxes in heterogeneous regions (Bougeault et tit. 1991 ). The patitioning of fluxes between the canopy and the soil requires a 'two layer' modelling approach wherein the fluxes from bare soil and the vegetation layer are estimated separately (Choudhury 1989). A wide suite of two layer models have been developed, especially in meteorology, at the scale of general circulation models (GCM) with varying degrees of complexity and at various spatial resolutions (e.g.. Deardorff 1978, Dickinson 1984. Shuttleworth and Wallace 1985, and Avissar and Picike 1989). While these two layer models have a sound theoretical basis, input variables such as surface resistance and temperature cannot be obtained separately for soil and vegetation components in large heterogeneous areas. Moreover, the current modelling schemes are inadequate to represent surface processes with any degree of confidence because of the complexity of interactions, the numerous requirements of data to initialize or validate these detailed models, and the data processing costs involved (Avissar and Verstraete 1990, Parlange cr al. 1995). Separating fluxes between canopy and soil surfaces permits the derivation of lEc, from the canopy and relate it to carbon assimilation and dry-matter accumulation (Choudhurv 1989). Since lEc is also an indicator of plant water consumption, a model is required to isolate the amount of water that is transpired from the canopy to obtain a realistic estimate of the plant's water requirement. This requires the parameterizing of the energy balance for vegetation and soil separately. In fact the objective of this paper is to present a method by which transpiration from vegetation alone can be estimated without the need for a complex two layer model. This specifically requires estimates of surface temperature and resistance to the transfer of fluxes from both layers independently. Since transpiration from land surface is directly influenced by the amount of vegetation, vegetation indices such as the Normalized Difference Vegetation Index (NDVI) which are correlated to vegetation cover could be related to the spatial and temporal variations in transpiration (Goward and Hope 1989, Choudhury et al. 1994). In this paper, we present a technique to model variations in transpiration with NDVI. The model is tested using data collected from the First ISLSCP Field Experiment (FIFE). RELATION BETWEEN NDVI AND SURFACE PARAMETERSNDVI and Canopy Temperature In order to calculate H from soil and vegetation separately, we need estimates of soil and canopy temperatures in equation (3). It has been shown by Goward and Hope (1989), Nemani and Running (1989), Price (1990), and Carlson et al. (1990) that a linear relationship exists between percentage of canopy cover on the ground and measured surface temperatures. Variations in green vegetation can be estimated from satellite observations by the increase in near-infrared reflectance (NIR) and decline in visible reflectance (VIS) that occurs with increasing leaf area index (LAI) (Tucker and Sellers 1986). These reflectances are usually expressed as 'Vegetation Indices', the most common one being the Normalized Difficrence Vegetation Index (NDVI) which is defined as
When the difference in reflectances in the visible and NIR regions are normalized as in equation (5). it tends to reduce the effects of changing sun or viewing angle (Holben 1986, Carlson et al. 1990). NDVI has been shown to be well correlated with net primary productivity, percentage of absorbed photosynthetically active radiation, and LAI (Sellers 1985, Tucker and Sellers 1986, Prince 1991 ). An analysis of the surface temperature data suggests that in general the vegetated areas are relatively cooler than the non-vegetated areas (Price 1990). This difference can be attributed to the marked difference in evapotranspiration and the thermal properties of bare soil and vegetation. Scatterplots of NDVI versus measured surface temperatures show a strong negative relation between the two variables. and the axis of the sloping distribution of points defines the variation of vegetation fraction with surface radiometric temperature (figure 1). If the land surface is a heterogeneous mixture of bare soil and vegetation, then the NDVI and surface temperature (T) measurements derived from a coarse resolution sensor such as AVHRR, can be expressed as follows (Price 1990. Nemani et al. 1993):
where the subscripts 0, c and s represent the variables measured over a mixed surface, full canopy and bare soil respectively. Thus, T0, and NDVI0 measured from the satellite at a coarse resolution can be considered as a linear mixture of contributions from the canopy and bare soil weighted by their fractional amount in each pixel. Although the relation between radiance measured by the sensor and surface temperature is non linear according to Planck's law, for the small range of surface temperatures observed here, it is reasonable to assume a linear relation between the two. This relation between NDVI and T0 is not unique to prairie grasses alone, and such relations have been observed over agricultural areas as well over different forest types (e.g. Price 1990, Nemani et al. 1993, Nemani and Running 1989). Extrapolating the regression line to the NDVI of bare soil and full canopy provides their respective surface temperatures. The NDVI of bare soils typically ranges between 0.0 and 0.2 depending upon soil brightness and moisture content (Heme 1989), and reaches an upper limit of approximately 0.8 over densely vegetated areas (Goward et al. 1994). Nemani et al. (1993) report that NDVI measurements from AVHRR varied between 0.28 and 0.65 for forests, 0.1 and 0.64 for crops, and 0.05 and 0.55 for grasses. Sensor calibration, cloud contamination, atmospheric affects, and surface anisotropy strongly influence NDVI measurements from AVHRR (Goward et al. 1991). By extrapolating the NDVI-surface temperature relation to the NDVI of a full canopy, the surface temperature over an area with complete canopy cover (canopy temperature) can be estimated. Canopy temperature (T) measured in this manner could be combined with air temperature measurements from standard meteorological stations, and knowledge of surface roughness to model sensible heat flux using equation (3) from the vegetation layer and the soil layer separately. The same surface temperature can also be used to estimate the upwelling longwave radiation from the two layers. NDVI and Transpiration Several studies in the past have used vegetation indices such as the NDVI or the Simple Ratio (SR = NIR/VIS) to quantify vegetation density as a function of the total leaf area index (LT) and photosynthetic activity of vegetation (e.g., Asrar et al. 1984, Daughtry et al. 1992). Sellers ( 1985, 1987) used a two-stream radiative transfer model to describe variations in NDVI and SR with photosynthesis and transpiration. The theoretical basis for his modelling is based on the work of Jarvis (1976), Charles-Edwards and Ludwig (1974), and Farquhar et al. (1980). The mechanics of the model operate on the principle that the photosynthetic rate (Ac) and stomatal conductance (gc) are driven by the fraction of Photosynthetically Active Radiation absorbed by the canopy (FPAR). Since NDVI and SR are known to be correlated to FPAR and LT which in turn influence Ac and gc it follows that Ac and gc can also be expressed as a function of NDVI:
Hence, spatial variability in NDVI indicates differences in leaf area index, photosynthetic rates and stomatal conductance. The above relations are of much importance in rernole sensing. since they can quantify the measurements of Ac and lEc with NDVI. Thus, if we know the relation between canopy conductance and vegetation density expressed by the magnitude of NDVI, then scaling transpiration at different NDVIs is feasible for a given cover type. Using the empirical relation between NDVI and stomatal conductance over FIF17 fiom Gao et al, (1992) values of lEc, were simulated for a range of canopy temperatures following equation (4) (figure 2). Figure 2 shows the dependence of lEc, on NDVI at different canopy temperatures. If all the vegetation were transpiring equalb, (i.e., resistance is uniform), then under similar environmental conditions, they would hme the same canopy temperature and the spatial variation in lEc, would then depend only upon the changes in vegetation density as indicated by NDVI. These assumptions are quite valid over small geographic units where the key environmental parameters such as air temperature, relative humidity and radiation that control lEc, do not vary substantially over the limited space. For example, the spatial variability of air temperature and vapor pressure deficit over the FIFE area was about 1?C and 1.5 millibars respectively during the two days when this analysis was conducted. Thus, at the same NDVI, higher rates of transpiration at higher temperatures indicate variations in transpiration in different environments. Figure 2 also shows that the lEc curves for different surface temperatures follow similar polynomial increase, indicating that the magnitude of change in lEc with vegetation density (NDVI) would always be similar for a given canopy temperature. This call be seen in figure 3, where lEc estimated at different NDVIs is expressed as a fraction of lEc from a full canopy for the prau ic grass ccosystern at the FIFE site. In this analysis. the NDVI of a full canopy was assumed to be 0.72, with visible and near-IR reflectance values of 0.06 and 0.38 respectively for a typical green canopy as derived by Monteith and Unsworth (1990) using the Kubelka-Munk equations. NDVI measurements from field observations during FIFE varied from 0.65 to 0.85 with much of the variability caused due to surface anisotropy (Deering et al. 1992, Russell et al. 1995). The relation between NDVI and lEc in figure 3 shows that under uniform environmental conditions water loss by transpiration varies as a function of vegetation density. Once the relation between NDVI and gc is established, similar relations between lEc and NDVI can be derived for several other vegetation species as well. The relation in figure 3 has important implications in estimating transpiration from satellite data. since it provides us with a functional relation to estimate spatial variations in lEc from NDVI, once lEc from a full canopy is known. The most crucial part however, is to predict lEc over the full canopy accurately. Otherwise, large errors in lEc could propagate when scaled from one NDVI to another. Gao et al. ( 1992) derived a linear relation between simple ratio (SR) and canopy conductance. However. a one-to-one correspondence exists between SR and NDVI following the formula SR = (1 + NDVI) (1 - NDVI). and we have used the relations between NDVI and canopy conductance only for convenience. Using SR or NDVI in the model does not make any difference. We have used NDVI instead of SR since it is it more widely used parameter to describe land surface characteristics. Also, the nature of relations between NDVI and transpiration (figure 3) is not effected by the range of NDVI used in the simulation. The relations between the fraction of (lEc/lEc0.72NDVI)and NDVI in figure 3 are best described by a third degree polynomial equation:
Field studies by Brun et al. (1971). Ritchie and Burnett (1971) and Kristensen 1974) show a similar non linear increase in transpiration with vegetation density. Choudhury ( 1994) and Choudhury et al. ( 1994) observed similar relations between transpiration and vegetation indices from field observations over several field crops. Lower values of NDVI correspond to lower values of LT and lower values of LT result in partitioning of the net radiation more to the soil than to the canopy. The following sections describe the validation of the model using data collected during FIFE. MODEL VALIDATION OVER FIFEThe FIFE study was conducted over a 15 km by 15 km test site near Manhattan, Kansas. The land cover of the site is predominantly prairie grass, over which meteorological, biophysical and hydrological measurements were made from remote sensing platforms as well as on the ground over a period extending from early 1987 through October 1989. An overview of FIFE is given by Sellers et al. (1992a). Four intensive field campaigns (IFCs) were held in 1987, and one in 1989 during which measurements of surface energy and carbon dioxide fluxes were made along with parameters of surface biology and atmosphere. These measurements were made at different spatial and temporal resolutions and were coordinated such that observations made at the surface would coincide with those made from remote sensing platforms. These data sets were readily available from the oil-line FIFE information system FFIS) at NASA Goddard Space Flight Center in Greenbelt, Maryland along with documentation (Strebel ei al. 1991). Data from the first and third IFC's was used in this study. Data from summer of 1987 were used in this experiment to derive lEc over FIFE. AVHRR-LAC images were examined from 26 May through 21 August and four days were chosen from this time period since they had minimal cloud cover and low satellite view angles. The four days are: 15 May, 6 June, 15 August. and 21 August. Of these four days, 6 June and 15 August were identified as 'Golden days' by the FIFE processing tearn since these were the best days during the IFC's on which data processing was given the highest priority because all field measurements were available and these days also had clear sky conditions. However, there were only two days (6 June and 21 August) during which reliable soil moisture and flux measurements were made simultaneously at the same ground stations and only data from these two days only were used in this study. Measurements of soil moisture are required to model flux measurements from the soil surface since these will enable partitioning of lEc between the soil and vegetation components separately. Simultaneous measurements of surface flux and soil moisture were made on both the days at site No. 26. At site No. 18 these measurements are available on 21 August only. Soil moisture was measured using impedance probes (Ungar et al. 1992), while the flux measurements were made by the Bowen ratio method. For the two days, AVHRR-LAC images were calibrated (Che and Price 1992), screened for clouds (Saunders 1986) and corrected for atmospheric effects in the visible and thermal bands (Tanie et al. 1990, Becker and Li 1990). NDVI, surface temperatures, and albeclos were calculated from these images and these values were extracted from a 20km by 20km window around the FIFE study site. The visible and NIR bands were used to derive the broad band albedo using the coefficients of Saunders (1990). NDVI was regressed against temperature values and the regression equations were used to estimate the surface temperature over a full canopy having an NDVI of 0.72 (figure 1). The temperature measurements estimated at an NDVI of 0.72 were used to estimate the outgoing long wave radiation (LW
where s = 5.67 x 10-8 W m-2 K-4 (Stefan-Boltzmann constant), e = 0.98 (emissivity measured over FIFE). and T = surface temperature (deg K). Average incoming shortwave and long wave radiation measurements that coincide with the time of satellite overpass were obtained from tile network of ground instruments within the FIFE site. These measurements along with the albedo and canopy temperatures derived from AVHRR as described above were used to estimate net radiation following (2). Sensible heat flux (11) over the full canopy was calculated using (3) from surface temperatures derived from the NDVI-surface temperature regression analysis (figure 1) and air temperature measured on the ground. Air temperature was measured on the ground every half hour using twelve automatic meteorological stations within the FIFE site (Betts and Ball 1995). The aerodynamic resistance was estimated as a function of wind speed following the empirical relationship between the two as derived by Verma et al. (1992) over FIFE. No stability corrections were performed since Vining and Blad (1992) have shown that stability corrected estimates of H were not in good agreement with the fluxes measured using the Bowen ratio (13) method over FIFE under moderate to low wind speeds. The canopy temperature estimated from the regression analysis of NDVI and surface temperature is very close to the air temperature (Prince and Goward 1995, Prihodko and Goward 1997), and as expected H is small over the full canopy (table 1). Modelled values of Rn and H were used to calculate lEc as a residual in (1). Table 1 gives the components of the energy balance equation for the two days over FIFE. The relations in figure 3 was used to adjust lEc from the full canopy to an average lEc value around the flux sites (Nos. 18 and 26) from which ground reference data was obtained for validation of this technique. To avoid errors caused by uncertainties in choosing the pixels that contain the ground measurements, a mean NDVI value from a 3 by 3 pixel area around the sites was used for this adjustment on each of the test days. The land cover within the 3 by 3 pixel window was fairly homogenous, and the surface temperature and NDVI within the window varied by 1.5 K, and 0.05 respectively. It should be remembered that the modelled values of lEc are from transpiration by the canopy alone (single source), while the flux station on the ground measures lE (lE = lEc + lEsoil) from both the canopy as well as from the soil surface (two sources). For the same reason, modelled values of transpiration from a full canopy cannot be directly compared with lE from the flux site. Hence, the evaporation from the soil and transpiration from vegetation have to be summed and then compared to the composite flux measurements from the sensors on the ground. Evaporation from the soil was modelled using the simple biosphere model (SiB) (Sellers et al. 1986) and added to the transpiration values estimated before. Soil moisture and temperature data required to run SiB were obtained from ground measurements at sites No. 26 and No. 18. The formulation used to estimated evaporation of water from the topmost soil layer is given by Sellers et al. (1992b):
where lEsoil = evaporation from the soil, W m-2; e*(Tgs) = saturated vapor pressure at soil temperature, Pa; h = relative humidity in soil pore space; ea = vapor pressure in the canopy air space, Pa; rsurf = soil surface resistance, s m-1; ra = aerodynamic resistance between soil surface and canopy air space, s m-1; r, Cp = density and specific heat of air respectively, kg m-3, J kg-1 K-1; g = psychrometric constant, Pa. The model variables in equation (10) were derived from soil physical properties measured during FIFE. and rsurf is estimatcd as an exponential function of soil moisture (Sellers er al. 1992 b). lEc derived from satellite data. and lEsoil estimated from SiB were summed to compute lE and these results are compared with the ground measurements of lE in table 2. It should be emphasized that SiB estimates of soil evaporation are used for validation purposes only, and estimation of lEc does not require inputs from SiB. Table 2 shows that the modelled values of lEc are within 10 per cent of ground measurements. However, it should also be noted that the ground measurements themselves may have a certain degree of uncertainty or error involved, and uncertainties in ground observations should be considered while comparing modelled values and ground measmements. Nie et al. (1992) compared measurements of Rn, lEc and b made from different instruments at the same time and at the same sites over FIFE, and have shown that on a daily basis, different instruments can make a difference of up to 10, 20 and 30 per cent in Rn, lEc and b respectively. However, for most of the sites, the differences in lEc measured from different instruments were less than 10 pet cent. Considering the uncertainty in the ground measurements, the modelled estimates of lEc compare well with the ground observations. These results provide evidence to support the theoretical arguments suggesting that if lEc over a full canopy can be accurately calculated, then it can be scaled to other areas having different canopy cover under similar environmental conditions provided the density of vegetation is known and expressed in terms of the NDVI. It should be noted that the estimated lEc is the sum of outputs from two different models, and it is difficult to validate the individual model outputs since sufficient data is not available front field measurements to do so. The transpiration model developed here provides a technique to model variations in lEc between different values of NDVI; however it is not clear how the soil evaporation would vary with canopy cover. While knowledge of transpiration is a key factor to study plant water requirements, estimating evapotranspiration is essential to study the overall energy balance of the land surface. The goal of this research was to design a method by which water consumption in plants could be monitored, and we have attempted to model flux measurements from the canopy layer only. POSSIBLE SOURCES OF ERRORModelling lEc accurately depends upon reliable estimation of lEsoil and lE from the soil and vegetation components separately. This again depends upon the ability of the NDVI and temperature relations to discriminate effectively between the soil and canopy temperatures. Absence of a good relation between NDVI and surface temperature will result in errors in estimating canopy temperature and could lead to large errors in estimating transpiration. For a well defined relation between NDVI and surface temperature, the land surface has to be a heterogeneous mosaic of vegetation and bare soil, and the images have to be cloud free, so that a wide range of NDVI and surface temperatures exist. If the vegetation cover is very uniform then the temperatures of bare soil and canopy cannot be resolved. Clouds and moist soil have low values of NDVI and are also cooler than dry soils. Therefore, the accuracy of canopy temperature retrieval depends upon surface inhomogeneity, soil moisture and cloud conditions in the image. Since NDVI is used as a surrogate for vegetation density, deriving an accurate relation between NDVI and lEc is very important for this model. lEc is very sensitive to NDVI, especially beyond an NDVI value of 0.6 because of the nonlinear relationship between them. Differences in calibration coefficients and atmospheric correction techniques will result in different values of NDVI and surface temperatures, and unless both of these parameters are accurate large errors could propagate through the model. Kalluri and Dubayah (1995) have shown that the differences belween ground measurement of satellite retrieved surface temperatures from AVHRR could be as much as 5 K. These differences could be caused due to either the empirical nature of the atmospheric correction schemes or because of the uncertainties in estimating the land surface emissivity. In spite of these limitations the modelled values of lEc compare well with measurements made on the ground. SENSITIVITY ANALYSIS OF THE TRANSPIRATION MODELSince there are several variables involved in the computation of lEc it is important to know the sensitivity of the model to the various inputs. This information will help in identifying the accuracy with which the individual variables have to be measured and the uncertainty in the final modelled output. The influence of any single variable on the computation of lEc can be studied by obserNing the changes in lEc caused by changes in the same variable when the other inputs to the model are kept constant. This numerical analysis call be performed by computing the partial derivatives of lEc with respect to the individual variables in equation (11). The pal tial derivatives of lEc can be used to separately model changes in lEc (?lEc)as a function of changes in individual input variables when all the other variables are kept constant. Table 3 gives the values of ?lEc when a single variable is changed. The values used in the computations are: SW It can be seen from table 3 that lEc is most sensitive to the changes in surface and air temperature values. A 1 K temperature difference between the air and surface temperature could lead to 34.74 W m-2 change in lEc. While the air temperature can be measured on the ground to an accuracy of within 1 K, it is not yet possible to estimate the surface temperature with the same degree of accuracy from satellites. Uncertainties in the estimates of surface emissivity. atmospheric composition, satellite navigation and calibration could lead to a ?3 K uncertainty in the measurement of surface temperature (Cooper and Asrar 1989) which could result in errors greater than 100 W m-2 in the estimation of lEc. Another important variable to which lEc is very sensitive in this model is the aerodynamic resistance (ra). ra can be accurately estimated when the ground cover is uniform. However, for areas with heterogeneous ground cover or in areas where the ground cover is incomplete, it is difficult to estimate ra since differences in roughness and stability conditions have to be accounted for (Kustas et al. 1990). SW Once the sensitivity of the model to various input parameters is known, it is easy to find out what the overall error in the estimate of lEc would be in a worst case scenario when all the variables involved in the computation of lEc have errors in them. The overall error in lEc can be assessed by performing an analysis of the propagation of errors. Thus, if lEc can be expressed as where v1, v2, v3...vk are the true variables used in the computation of lEc, then lEc when calculated with variables which have errors in them can be expressed as: where s1, s2, s3...sk are the errors in the variables v1, v2, v3...vk respectively. Following the Taylor seriesm, the absolute error (s.d.(l?c)) involved in the computation of lEc, which is the difference between lEc and l?c, can be expressed as: where si is the error in the variable vi. The values of ?Ec/?vi are given in table 3. Thus, knowledge about the uncertainty in the individual measurements can be combined with the sensitivity of the model to the individual variables to measure the overall error in the computation of lEc following equation (14). When the errors in SW However, the value of s.d.(lEc) derived here is for a worst case scenario, and typically, the errors involved in the computation of lEc are much smaller than for a worst case. Comparison of modelled values of lEc with ground measurements over FIFE indicate that the errors are less than 9 per cent in this study (table 2), a significant reduction from the worst case scenario. This indicates that the algorithms used in this research to derive the variables required for the computation of lEc resulted in smaller uncertainties in the variables used leading to a higher accuracy in the modelled values of lEc. The relation between transpiration and NDVI is given by a third order polynormal equation (8). and the rate of change of transpiration with NDVI is not constant due to the non linearity of the relations. According to this model, variations in transpiration are more sensitive at higher values of NDVI, and the sensitivity of the predicted variable can be determined from the derivative of equation (8): The model developed here describes variations in canopy transpiration as a function of NDVI. The differences between modelled instantaneous values of lEc and ground measurements were less than 10 per cent during FIFE. The nonlinear relation between transpiration and NDVI shows that simple linear additive models may not be sufficient to describe variations in evapotranspiration with vegetation density. However, the relation between NDVI and lEc is unique to different vegetation types (e.g., C3 and C4), and the appropriate relations should be developed from relevant plant physiological attributes. While the relation between lEc from the canopy component and NDVI has been established, it is not yet clear how the evaporation component from the soil would vary with fractional vegetation cover. Although it is expected that the soil evaporation would diminish with increasing NDVI when there is no irrigation, no attempt is made here to develop a quantitative relation between NDVI and bare soil evaporation. This issue needs to be researched in detail so that a realistic estimate of the land surface energy balance can be obtained. Because of the nonlinear relation between NDVI and lEc this model is very sensitive to the magnitude of NDVI, especially beyond an NDVI of 0.6. Thus, errors in the estimation of NDVI and Tc could resuit in large errors in modelling lEc. For the same reason particular attention should be paid in calibration and atmospheric correction of satellite data. While a pixel by pixel calculation of energy fluxes is desirable, parameterizing the surface resistance values is very difficult at the pixel level. No unique solution exists for this problem, especially in heterogeneous areas where there is a mixture of different cover types with varying proportions of canopy cover. The model developed here works well when the surface temperature over a full canopy and bare soil can be independently and accurately parameterized for reasons already discussed in POSSIBLE SOURCES OF ERROR. This is possible through the linear relation between NDVI and surface temperature. Such a relation exists only in a heterogeneous landscape having a wide range of NDVT and surface temperature values. While day to day variations in NDVI are negligible, variations in lEc can be substantial depending upon the prevailing environmental conditions and water availability to the plants. Plant canopy temperatures indicate the onset and degree of stress at a particular time, while the effect of stress over a long time can be monitored through the use of vegetation indices (Campbell and Norman 1990). Thus, maximum value NDVI composites may help identify areas over which vegetation is actively growing and areas with retarded growth because of water stress or other vegetation conditions, but there may not be any indication as to the degree of stress or the amount by which lEc is falling short of the potential values required for the proper growth of the plant. The methodology developed here can be effectively used to study spatial and temporal patterns in lEc to understand the energy balance of vegetation in global climate change and agricultural studies. It can also be used to detect the onset, degree and duration of water stress in crops and other vegetation. The results from this research emphasize the synergism of land surface evaporation and multi-spectral measurements. It has been shown in SENSITIVITY ANALYSIS OF THE TRANSPIRATION MODEL that lEc is very sensitive to surface temperature, albedo and aerodynamic resistance values. Measurements of surface temperature and albedo can be improved if accurate information is available regarding surface emissivity, atmospheric composition and satellite calibration. Thus, in order to implement this model operationally we need surface temperature and reflectance measurements which are well calibrated and corrected for atmospheric effects. The authors wish to thank Sam Goward, Steve Prince, Neal Barnett, and Ralph Dubavah for their advice in this research. Richard Strub of USDA provided technical assistance. We are grateful to Mark Heiser for providing us with SiB cstimatcs of soil evaporation, and Paul Smith for his help in the sensitivity analysis. The Goddard DAAC provided the FIFE data. Satya Kalluri was supported by the University of Maryland at College Park on a graduate research assistantship during the time of this research. We appreciate the valuable comments of the two anonymous reviewers. ASRAR, G., FUCHS, M., KANEMASU, E. T., and HATFIELD, J. L., 1984, Estimating absorbed photosynthetic radiation and leaf area index from spectral reflectance in wheat. Agronomy Journal, 76, 300 306. AVISSAR, R., and PIELKE, R. A.. 1990, A parameterization of heterogeneous landsurface for atmospheric numerical models and its impact on regional meteorology. Monthly Weather Review, 117, 2113 2136. AVISSAR, R., and VERSTRAETTE, M. M., 1990, The presentation of continental surface processes in atmospheric models. Reviews of Geophysics, 28, 35 52. BALL, J.T., 1988, An analysis of stomatal conductance. Ph.D. Thesis, Stanford University. BECKER, F., and Li, Z. L., 1990, Towards a local split window method over land surface. International Journal of Remote Sensing, 11, 1509 1522. BETTS, A.K., and BALL. J.T., 1995. The FIFE surface diurnal cycle climate. Journal of Geophisioal Research. 25, 25 679 25 693, BOUGEAULT, T.P., BRET, B., LACARRERE, P., NOILHAN, J., 1991, An example of spatial integration of a land-surface patameterization in meso-beta-scale model. In Land Surface Evaporation edited hy F J. Schmuggc. and J, Andre (New York: Springon-Verlag). pp. 383 410, BRUN, L.J., KANEMASU, E.T., and POWERS, W.L., 1973, Estimating transpiration resistance. Agronomy Journal. 65, 326-328, CAMPBELL, G. S., and NORMAN, J. M., 1990. Estimation of plant water status from canopy temperature: an analysis of the inverse problem. In Application of Remote Sensing to Agriculture edited by M. D. Steven. and J. A. Clark (London: Butterworths). pp.255-271. CARLSON, T.N., PERRY, E.M., and SCUMUGGEE, J.T., 1990, Remote estimation of soil moisture availability and fractional vegetation cover for agricultural fields. Agricultural and Forest Meteorology, 52, 45 69. CHARLES-EDWARDS, D. A., and LUDWIG, L.J. 1974, A model for leaf photosynthesis by C3 plant species. Annals of Botany, 38, 921-930. CHE, N., and PRICE, J.C.- 1992. Survey of radiometric calibration results and methods for visible and near infrared channels of NCAA-7. -9 and -11 AVHRRs. Remote Sensing of Environment - 41, 19 28. CHOUDHURY, B.J., 1989, Estimating evaporation and carbon assimilation using infrared temperature data: Vistas in modelling. In Theory and Applicalions of Optical Remote Sensing edited bv G. Aster (New York: John Wiley and Sons), pp. 628-690. CHOUDHURY, B. J. 1994. Synergism of multispectral satellite observations for estimating regional land surface evaporation. Remote Sensing of Environment, 49, 264 274. CHOUDHURY, B. J. AHMED, N. U., IDSO, S. B., REGINATO, R. J., and DAUGHTRY, C. S. T., 1994, Relations between evaporation coefficient, and vegetation indices studied by model simulations. Remote Sensing of Environment, 50, 1-17, COOPER, D. I., and ASRAR, G., 1989, Evaluating atmospheric correction models for retrieving surface temperatures from the AVHRR over a tallgrass Prairie. Remote Sensing of the Environment, 27, 93-102. COWAN, I. R., 1982, Regulation of water use in relation to carbon gain in higher plants. In Physiological Plant Ecology II edited by 0. L. Lange, P. S. Nobel, C. B. Osmond, and H. Ziegler (New York: Springer-Verlag), pp. 589 613. DAUGHTRY, C. S. T., GALLO, K. P., GOWARD, S. N., PRINCE, S. D., and KUSTAS, W. P., 1992, Spectral estimates of absorbed radiation and biomass production in corn and soybcan canopies. Remote Sensing of Environment. 39, 141 152, DEARDORFF, J. W., 1978. Efficient prediction of ground surface temperature and moisture with inclusion of layer of vegetation. Journal of Geophysical Research, 83, 1889 1903. DEERING, D. W., MIDDLETON, E. M., IRONS, J. R., BLAD, B. L., WALTER-SHEA, E. A., HAYS. C. J., WALTHALL, C., ECK, T. F., AHMAD, S. P., and BANERJEE, B. P., 1992, Prairie grassland bidirectional reflectances measured by different instruments at the FIFE site. Journal of Geophysical Research. 97, 18 887 18 903. DICKINSON, R. E., 1984. Modelling evapotranspiration for three dimensional global climate models. In Climate Processing and Climate Sensitivity. American Geophysical I Union Monograph. Vol. 29 (Washington DC: AGUL pp. 58-72. FARQUHAR. G. D., VON CAEMMERER, S., and BERRY, J. A., 1980, A biochemical model of photosynthetic C02 fixation in leaves of C3 species. Planta, 149, 78-90. GA0, W., WESLEY, M. L., COOK, D. R., and HART, R. L., 1992. Air-surface exchange of H20, CO2 and 03 at a tall grass prairie in relation to remotely-sensed vegetation indices. Journal of Geophysical Research, 97, 18 663 18 672. GOWARD, S. N., and HOPE, A. S., 1989, Evapotranspiration from combined reflected solar and emitted terrestrial radiation: Preliminary FIFE results from AVHRR data. Advances in Space Research 9, 239-249 GOWARD, S. N., MARKHAM, B., DYE, D. G., DULANEY, W., and YANG, J. 1991. Normalized difference vegetation index measurements from the advanced very high resolution radiometer. Remote Sensing of Environment, 35, 257-277. GOWARD, S. N., TURNER, S., DYE, D. G., and LIANG, S., 1994. The University of Maryland improved Global Vegetation Index product. International Journal of Remote Sensing, 15, 3365 3395. HEUTE, A. R. 1989. Soil influence in remotely sensed vegetation spectra. In Theory and Appluations of Optical Remote Sensing edited by G. Asrar (New York: John Wiley and Sons), pp. 107 141. HOLBEN, B. N., 1986. Characteristics of maximum-value composite images from temporal AVHRR data. International Journal of Remote Sensing, 7, 1417-1434 JACKSON, R. D., 1985. Evaluating evapotranspiration at local and regional scale. Proceedings of the I.E.E.E., 1086 1096. JACKSON, R. D., IDSO, S. B., REGINATO, R. J., and PINTER, P. J., 1981, Canopy temperature as a crop stress indicator. Water Resources Research, 4, 1133-1138. JARVIS, P. G., 1976. The interpretations in the variations in leaf water potential and stomatal conductance found in canopies in the field, Philosophical Transactions of the Royal Society Of London, series B, 273, 593-610. KALLURI S. N. V., and DUBAYAH, R. 0., 1995, Comparison of atmospheric correction models for thermal bands of the advanced very high resolution radiometer over FIFE. Journal of Geophysical Research, 100, 25 411 15 418. KUSTAS, W. P., MORAN, M. S.. JACKSON, R. D., GAY, L. W., DUELL, L. F. W., KUNKEL, K. E., and MATTHIAS. A. D., 1990, Instantaneous and daily values of the surface energy balance over agricultural fields using remote sensing and a reference held in an arid environment. Remote Sensing of Environment, 32, 125 141 KRISTENSEN, K. J., 1974, Actual evapotranspiration in relation to leaf area. Nordic Hydrology, 5, 173 182. MONTEITH, J. L., and UNSWORTH, M. H., 1990. Principles of Environmental Physics, London: Edward Arnold). NEMANI, R. R., and RUNNING, S. W., 1989, Estimation of regional surface resistance to evapotranspiration from NDVI and thermal-IR AVHRR data. Journal of Applied Meteorology, 28, 276-2S4. NEMANI, R. R., PIERCE, L., RUNNING, S. and GOWARD, S. G., 1993, Developing satellite-derived estimates of surface moisture status. Journal of Applied Meteorology, 32, 548-55T NIE, D., KANEMASU, E. I., FRITSCHEN, L. J., WEAVER, H. L., SMITH, E. A., VERMA, S. B., FIELD, R. T., KUSTAS, W. P., and STEWART, J. B., 1991 An intercomparison of surface energy flux measurement systems used during FIFE 1987. Journal of Geophysical Research, 97, 18 715 18 724. NOBEL, P. S., 1983, Biophysical Plant Physiology and Ecology San Francisco: W. H. Freeman Lind Cut. O'TOOLE, J. C., TURNER, N. C., NAMUCO, 0. P., DINGKUHN, M., and GOMETZ, K. A., 1984, Comparison of some crop water stress measurement methods. Crop Science, 24, 1121-1128. PARLANGE, M. B., EICHINGER, W. E., and ALBERTSON, J. D., 1995, Regional scale evaporation and the atmospheric boundary layer. Reviews of Geophysics. 33, 99 124. PRICE, J. C., Using spatial context in satellite data to infer regional scale evapotranspiration. I.E.E.E. Transactions in Geosciences and Remote Sensing. 28, 940 948. PRIHODKO, L., and GOWARD. S. N., 1997. Estimation of air temperature from remotely sensed surface observations. Remote Sensing of Environment, 60, 335 346 PRINCE, S. D., 1991, A model of regional primary production for use with coarse resolution satellite data. International Journal of Remote Sensing, 12, 1313 1330. PRINCE, S. D., and GOWARD, S. N., 1995, Global primary production: a remote sensing approach. Journal of Biogeography, 22, 815 835, RITCHIE, J. T., and BURNETT, E., 1971, Dryland evaporative flux in subhumid climate: II. Plant influences. Agronomy Journal. 63, 56 62. RUSSELL, C. A., WALTHALL, C. L., IRONS, J. R. and BROWN DE COLSTOUN, E. C., 1995, Comparison of airborne and surface bidirectional reflectance factors, spectral bemispherical reflectance and spectral vegetation indices. Journal of Geophysical Research. 100, 25 509 25 522. SEGUIN, B., and ITIER, B., 1983, Using midday surface temperature to estimate daily evaporation from satellite thermal IR data. International Journal of Remote Sensing. 4, 371 383. SAUNDERS, R. W., 1986, An automated scheme for the removal of cloud contamination from AVHRR radiances over Western Europe. International Journal of Remote Sensing, 7, S67 886, SAUNDERS, R. W., 1990, The determination of broad band outface albedo from AVHRR visible and near-infrared radiances. International Journal of Remote Sensing, 11, 49 68, SELLERS, P. J., 1985, Canopy reflectance, photosynthesis, and transpiration. International Journal of Remote Sensing, 6, 1335- 1371. SELLERS, P. J., 1987. Canopy reflectance, photosynthesis, and transpiration: II. The role of Biophysics in the linearity of their interdependence, 1987. Remote Sensing of Environment, 21, 143 183. SELLERS, P. J.. MINTZ, Y., SUD, Y. C., and DALCHER, A., 1986, A simple biosphere model (SiB) for use within general circulation models. Journal of Atmospheric Science. 43, 305 331. SELLERS, P. J., HALL, F. G., STREBEL, D. E., ASRAR, G., and MURPHY. R. E., 1992a, An overview of the first international satellite land surface climatology project (ISLSCP) field experiment (FIFE). Journal of Geophysical Research, 97, 18 345- IS 371. SELLERS, P. J., HEISER, M. D., and HALL, F. G., 1992b, Relations between surface conductance and spectral vegetation indices at intermediate (100 m2 to 15km2) length scales. Journal of Geophysical Research, 97, 19 033 19 060. SHUTTLEWORTH, W. F. and WALLACE, J. S., 1985, Evaporation from sparse crop-- an energy combination theory. Quarterly Journal of Royal Meteorological Society. 111, 839-855. SMITH, E. A., CROSSON, W. L., and TANNER, B. D., 1992. Estimation of surface heat and moisture fluxes over a prairie grassland 1. In situ energy budget measurements incorporating a cooled mirror dew point hygrometer. Journal of Geophysical Research, 97, 18 557-18 682. STREBEL, D. F., LANDUS, D., NEWCOMER, J. A., DECAMPO, J., and MEESON, B. W., 1991, Collected Data of the First ISLSCP Field Experiment. NASA, Goddard Space Flight Center. M.D. TANNER, C. B., 1981. Transpiration efficiency of potato. Agronomy Journal, 73, 59 64. TANNER, C. B. and SINCLAIR, T. R. 1983. Efficient water use in crop production: Research or research? In Limitations to Efficient Water Use in Crop Production edited by H. M. Taylor, W. R. Jordan, and T. R. Sinclair (Madison: American Society of Agronomy), pp. 1-28. TANRE, D., DEROO, C., DUHAUT, P., HERMAN, J. J., MORCRETTE, J. J. PERBOS, J. and DESCHAMPS, P. Y., 1990, Description of a Computer code to simulate the satellite signal in the solar Spectrum: the 5S Code. International Journal of Remote Sensing, 11, 659 668. TUCKER, C. J., and SELLERS, P. J., 1986, Satellite remote sensing of primary production. International Journal of Remote Sensing, 7, 1395 1416. UNGAR, S. G., LAYMAN, R., CAMPBELL, J. E., WALSH, F. and MCKIM, H. J., 1991. Determination of soil moisture distribution front impedance and gravimetric measurements. Journal of Geophysical Research, 97, 18 969-18 978 VERMA, S. B., KIM, J., and CLEMENT, R. L., 1992. Momentum water vapor and carbon dioxide exchange at a centrally located Prairie site. Journal of Geophysical Research. 97, IS 629-18 640. VINING, R. C., and BLAD, B. L., 1992, Estimation of sensible heat flux front remotely sensed canopy temperatures. Journal of Geophisical Research, 97, 18 951 18 954. WIT, C. T. DE, 1959, Transpiration and Crop Yields (Wageningen Institute of Biological and Chemical Research on Field Crops and Herbage). | |||||






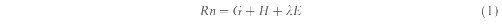
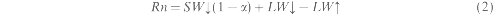
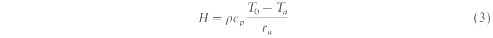
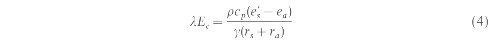
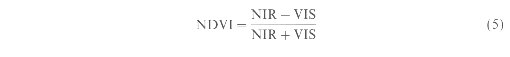
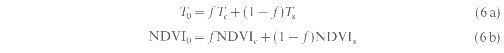
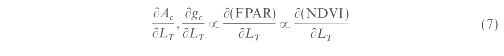
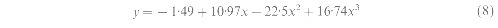
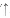 ) over the full canopy from Stefan-Boltzmann's equation:
) over the full canopy from Stefan-Boltzmann's equation: 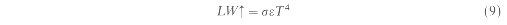
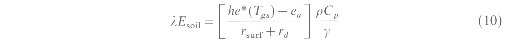
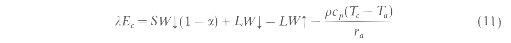
 = 850 W m-2, a = 0.16, LW
= 850 W m-2, a = 0.16, LW