ABSTRACT

A method is developed to estimate transpiration (T) by combining satellite and ground measurements. The method follows the energy balance approach where transpiration is estimated as a residual when net radiation (Rn), sensible (H) and soil heat (G) fluxes are known. The model estimates T from the vegetation layer only, and does not require a complex two layer model to separate the fluxes from the canopy and the ground layers. The method was validated using data collected during the First ISLSCP Field Experiement (FIFE), and the modeled values of evapotranspiration (ET) were within 9% of ground observations. The model was applied to data collected from four crop reporting districts in Iowa during 1988 to derive T and a Crop Water Stress Index. Model results successfully monitored the incidence, degree and duration of water stress among the different crop reporting districts.

INTRODUCTION

The ratio if actual evapotranspiration (ET) and potential evapotranspiration (PET) has been widely used to quantify water stress in vegetation [1],[2]. ET consists of evaporation (E) from the background soil layer and transpiration (T) from the vegetation layer. In heterogeneous areas where land cover is a mixture of bare soil and vegetation (which is usually the case), a "two layer" modeling approach is required, wherein the fluxes from bare soil and vegetation layer are estimated separately. This requires two energy budget equations, one for the vegetation, and another for bare soil.

Although a suite of two layer models exist [3],[4], the parameters required to run these models such as stomatal resistance and soil moisture are not readily available over large regions. A technique is developed here, to estimate T from the vegetation layer only without the need for a complex two layer model. The model allows the scaling of T as a function of vegetation density.

THEORY

The surface energy balance is written as:

where Rn is the net radiation, G is soil heat flux. H is the sensible heat flux, and ET is the latent heat flux due to E and T (ET=E+T). Rn is the sum of the incoming and outgoing fluxes at the surface, and can be written as: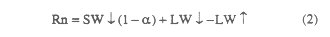

where SW is the shortwave radiation, a is the surface albedo, and LW is the longwave radiation. The up and down arrows indicate the direction of fluxes away and towards the surface respectively. The total daily magnitude of G is negligible over vegetated areas [5]. H and ET can be parameterized as: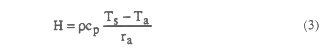

where rc_p is the volumetric heat capacity of the air (~1200 J m³ K^-1), T_s and T_a are the surface and air temperatures (K) respectively, and r_a is the aerodynamic resistance of the surface (s m^-1). H is dependent upon the magnitude of r_a, and the difference between the surface and air temperatures.

In (4) e'_s is the saturated vapor pressure (kPa) at T_s, e_a is the actual vapor pressure (kPa) at T_s, g is the psychrometric constant (-0.066 kPa K^-1), and r_s is the canopy resistance (s m-1). r. is the reciprocal of canopy conductance (gc). Rn, G, H, ET, SW and LW are expressed as Watts/m² (W/m²).

The partitioning of energy between H and ET depends on the availability of water to the plant. Under conditions where the water supply is not limited, most of the energy is partitioned towards ET, otherwise it is partitioned towards H. Reducing the water supply to plants results in an increase in canopy temperature, leading to an increase in H [6].

Normalized Difference Vegetation Index (NDVI) {NDVI=(NIR-VIS)/(NIR+VIS)}, derived from visible (VIS) and near-IR reflectances (NIR), has been widely used to estimate total leaf area index (LAI) [7], net primary productivity [8] and Fraction of Photosynthetically Active Radiation (FPAR) absorbed by the canopy [9]. Sellers [10] used a two-stream radiative transfer model to describe variations in NDVI with photosynthesis and T. The mechanics of the model operate on the principle that the photosynthetic rate (A_c), and g_c are driven by FPAR. Since NDVI is known to be correlated to FPAR and LAI [7], [9], which in turn influence A_c and g_c, it follows that A_c and _g can be expressed as a function of NDVI: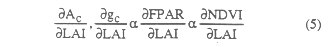

Thus, if we know the relationship between g_c and NDVI, then a functional relationship between T and NDVI can be derived which allows scaling of T at different NDVI.

TESTING THE MODEL OVER FIFE

Data collected during the First ISLSCP Field Experiment (FIFE) was used to test the validity of (5), and to derive a functional relationship between T and NDVI. Using the empirical relationship between NDVI and gc observed over FIFE [11], T was simulated for a range of canopy temperatures and NDVI (Fig.1). Fig.1 shows that there is a similar exponential increase in T with NDVI at different canopy temperatures, indicating that the magnitude of change in T with NDVI would always be proportional to the change in canopy temperature. This can be seen in Fig.2, where the ratio of T estimated at different NDVI and canopy temperatures, and T estimated over a full canopy at the same canopy temperatures is shown as a function of NDVI. Thus if NDVI, T, and canopy temperature of the vegetation layer are known, then T can be estimated for pixels with different NDVI values having the same canopy temperature. In this analysis, the NDVI of a full canopy was assumed to be 0.72 with typical visible and near-IR reflectances of 0.06 and 0.38 respectively for a green foliage [12]. Thus, if an area has varying amounts of canopy cover represented by varying NDVI, and if all the canopy elements were transpiring equally, T from the canopy layer within each pixel can be estimated from the relationship in Fig.2 if the T from a full canopy is known. A similar relationship between NDVI and E from the soil layer could be developed if the E from the bare soil and its NDVI are known. However, no attempt is made here to develop such a relationship for the soil component.

Figure One

The relationship derived in Fig.2 is similar to the relationship between T and LAI observed from field data by Brun et al.[13], and Kristensen [14], who have reported similar nonlinear increase in canopy transpiration with LAI. Also, Gao et al.[11] has shown that the partitioning of Rn towards ET increases compared to H with an increase in the NDVI over FIFE, indicating that soil influence decreases by an order of magnitude as the vegetation cover increases.

NDVI were derived from channel 1 and 2 reflectances of the Advanced Very High Resolution Radiometer (AVHRR) on board the NOAA-9 satellite for two clear days (June 6, and August 21, 1987) over FIFE. Surface temperature measurements were derived from channel 4 and 5 brightness temperatures [15]. Canopy temperatures for these two days were estimated using a linear regression between NDVI and surface temperatures [16]. Albedo of the FEFE site was estimated from channel 1 and 2 reflectances [17]. SW, LW, and r_a were obtained from ground measurements. Using these inputs, Rn and H were modeled for a full canopy using (2) and (3). Once Rn and H are known, T was estimated as a residual in (1). This is the transpiration from a full canopy.

Having known T from the canopy layer which has a hypothetical NDVI of 0.72, the next step was to estimate T over pixels within the same area having variable canopy cover represented by different NDVI values. To validate the model results, NDVI values were extracted for a 3 x 3 pixel area around two ground flux measurement stations in FIFE, and the T modeled over a full canopy was scaled to the NDVI around the flux sites following the relationship in Fig.2. However, the flux stations on the ground measure a combined ET from both the soil and canopy lavers. Thus, to compare the satellite estimates of T with ET measured on the ground, the contribution of E from the soil layer and the T from the canopy layer to the flux station measurements have to be estimated. The contribution of E from the soil layer was estimated using the Simple Biosphere Model (SiB) [18]. Table 1 shows modeled and measured values of ET over the two stations on the two days. On August 21, data from station No.18 was not reliable as the area surrounding it was water logged, and was excluded from the comparison.

These results provide evidence to support the theoretical arguments suggesting that if T over a full canopy can be accurately modeled, then it can be scaled to other areas having different canopy cover under similar environmental conditions using NDVL However. this argument is valid only if all the vegetation is transpiring at the same rate and has a similar canopy temperatures. Such an assumption is quite valid over small geographic areas where the environmental conditions do not vary spatially.

MODELING WATER STRESS OVER IOWA

After validating the transpiration model with ground measurements over FIFE, a similar study was carried out over five counties in the state of Iowa in the US Midwest region. The data used in this study is from 1988. The 1988 growing and harvest season was the driest on record, and had one of the worst droughts of the century in this region.

The five counties selected fall under four crop reporting districts (CRD): North West (NW), East Central (EC), Central (C), and South East (SE). Of these four crop reporting districts, NW had the least drought. while the rest experienced severe drought.

Eleven clear AVHRR images were selected for the growing season from May to August. All the images were screened for clouds, calibrated and corrected for atmospheric effects using the 5S radiative transfer code [19]. NDVI and surface albedo were estimated from the channel 1 and 2 reflectances [17]. Surface temperatures were estimated from channel 4 and 5 brightness temperatures [15]. Air temperature, wind speed, and relative humidity measurements were acquired from ground stations located within each county. SW estimates for each county were obtained from the GOES satellite [20]. LW was parameterized from air temperature and relative humidity measurements following Brutsaert [21]. Canopy temperatures within each county were estimated by regression analysis of NDVI and surface temperatures [16]. Using the above parameters Rn, and H were modeled for a full canopy within each county. Transpiration was estimated as a residual in (1), and scaled as a function of the average NDVI of the county, so that an average transpiration from the total canopy cover could be obtained. To scale T measured over a full canopy to an average value of the county, a functional relationship was modeled between T and NDVI as explained in TESTING THE MODEL OVER FIFE.

Table One

Corn and soybeans are the two predominant crops grown in Iowa. Data from Sellers [10], and Sellers et al. [22] was used to model the relationship between T and NDVI. Fig. 3 shows the modeled relationship between NDVI and the fractional change in T for corn and soybeans. These relationships can be best described by third degree polynomials:

As expected soybeans (C3) have a higher transpiration rate compared to corn (C4). Information regarding the fraction of corn and soybeans within each county was obtained from field reports, and T measured within each county was adjusted to give a weighted average transpiration using the mean NDVI of the county following (6a) and (6b).

Figure Three

The Priestly and Taylor [23] technique was used to estimate potential transpiration (Tp) within each county. From the modeled values of T and T_p a Crop Water Stress Index (CWSI) was calculated following Jackson et al.[1]:

CWSI has a range from 0 to 1. Under extreme stress conditions, T is very small and CWSI is close to 1, indicating maximum stress. When there is no stress, T and T_p would be equal, and CWSI will be close 0.

Fig.4 shows the temporal trend of CWSI from the four crop reporting districts along with the different phenological stages of com reported from the field. Since no measurements of either T or T_p were made in the field. the temporal trends of CWSI from the four crop reporting districts will be objectively analyzed by comparing them with the crop conditions reported in the field. CWSI cannot be correlated with any single environmental variable alone since it is influenced by a combination of several factors such as radiation, air temperature, relative humidity, soil moisture and crop growth stage, and because the interrelationship between these factors is again very complex.

The temporal profile of CWSI among the four crop reporting districts are similar in magnitudes until Julian day 185 (July 3). From this day onwards the increase in CWSI in the north west was lower compared to the other districts. Of the four crop reporting districts the north west received the highest amount of rainfall after Julian day 180, which helped to sustain the crops (Fig.5). Average precipitation was lower than the long term mean (1951-1980) throughout the state in June by 7.9 cm., and by 3.9 cm. during July. North west crop reporting district had the least deviation from the normal (5.8 cm.), while the east central had the highest deviation (9.1 cm) among the four crop reporting districts during June. The weekly weather bulletins; describe this period as 'hot and dry'.

Figure Four

Figure Five

Field conditions steadily deteriorated from about Julian day 190 in all the districts except the north west, and this is reflected in the CWSI profiles. Field reports also indicate that almost all areas in the state showed some wilting and drying of lower leaves in plants benveen days 207 and 213 (last week of July). Thunderstorms in the north west provided relief from days 221 to 227 (Fig.5), which rapidly brought down the CWSL

Very low moisture conditions accompanied by extreme temperatures may be very injurious to even C4 plants such as com. From the reproductive stage onwards, CWSI in the North western counties decreased substantially compared with the other parts of the state. Temperatures were cooler and rain fell among the other districts from day 225 onwards. But the rainfall was low and by that time it was too late to revive the crops in these districts although it benefited some soybean crops that were planted late. In some of the counties plants were cut for fodder and silage because of low grain production.

From a comparison of modeled CWSI and field reports of weather and crop conditions, it can be seen that CWSI was successful in predicting the degree and duration of water stress among the four crop reporting districts. Variations in CWSI follow variations in rainfall and agree well with ground information about crop conditions. Results from this research show that CWSI when analyzed in conjunction with information about crop growth stages may prove to be a valuable tool to help in crop and yield forecasting, since the time of incidence of stress, and its degree and duration can be used to identify areas with potential reduction in yield.

SUMMARY AND CONCLUSIONS

A new technique is developed here that combines satellite and ground measurements to estimate transpiration from the canopy layer. The method allows the scaling of transpiration as a function of canopy cover through NDVI. The method was tested over FIFE and the results were within 9% of ground measurements. This method was used to derive CWSI over four different crop reporting districts in Iowa. Temporal profiles of CWSI were successful in identifying the incidence, degree and duration of water stress in field crops. This method has a potential application in detecting water stress in agricultural areas, and can be operationally used over large areas.

ACKNOWLEDGMENTS

We wish to thank John Townshend, Ralph Dubayah, Sam Goward, Steve Prince, Neal Barnett, Richard Strub, and Mark Heiser for their valuable inputs and guidance in this research. The Goddard DAAC provided the FIFE datasets.

REFERENCES

[1] R. D. Jackson, S. B. Idso, R. J. Reginato and P. J. Pinter, "Canopy temperature as a crop stress indicator". Water Resources Research vol. 4, pp. 1133-1138, 1981.

[2] J. C. O'Toole, N. C. Turner, 0. P. Namuco, M. Dingkuhn, and K. A. Gometz, "Comparison of some crop water stress measurement methods", Crop Science, Vol. 24, pp. 1121-1128, 1984

[3] R. Avissar, and R. A. Pielke, "A parameterization of heterogeneous landsurface for atmospheric numerical models and its impact on regional meteorology", Monthly Weather Review, vol. 117, pp.2113-2136, 1989.

[4] J. W. Deardorff, "Efficient prediction of ground surface temperature and moisture, with inclusion of layer of vegetation", Journal of Geophysical Research vol. 83, pp. 1889-1903, 1978.

[5] W. P. Kustas, R. D. Jackson, and G. Asrar, 'Estimating surface energy-balance components from remotely sensed data", in Theory and Applications of Optical Remote Sensing, Ed. G. Asrar, NewYork, John Wiley and Sons, 1989.

[6] G. S. Campbell, and J. M. Norman. 'Estimation of plant water status from canopy temperature: an analysis of the inverse problem", Application of Remote Sensing to Agriculture, London, Butterworths, 1990.

[7] G. Asrar, M. Fuchs, E. T. Kanemasu, and J. L. Hatfield, "Estimating absorbed photosynthetic radiation and leaf area index from spectral reflectance in wheat", Agronomy Journal, vol.76, pp. 300-306, 1984.

[8] C. J. Tucker, and P. J. Sellers, "Satellite remote sensing of primary production" International Journal of Remote Sensing, vol. 7, pp. 1395-1416, 1986.

[9] C. S. T. Daughtry, K. P. Gallo, S. N. Goward, S. D. Prince and W. P. Kustas, "Spectral estimates of absorbed radiation and phytomass production in corn and soybean canopies", Remote Sensing of Environment, vol. 39, pp- 141-152, 1992.

[10] P. J. Sellers, "Canopy reflectance, photosynthesis, and transpiration" International Journal of Remote Sensing, vol. 6, pp. 1335-1371, 1985.

[11] W. Gan, M. L. Wesley, D. R. CoK and R. L. Hart, "Air-surface exchange of H20, C02, and 03 at a tail grass Prairie in relation to remotely sensed vegetation indices", Journal of Geophysical Research, vol. 97, pp. 18663-18672,1992.

[12] J. L. Monteith, and M. H. Unsworth, Principles of Environmental Physics, London, Edward Arnold, 1990.

[13] L. J. Brun, E. T. Kanemasu and W. L. Powers, "Estimating transpiration resistance", Agronomy Journal, vol. 65, pp.326-328, 1973.

[14] K. J. Kristensen, "Actual evapotranspiration in relation to leaf area", Nordic Hydrology, vol. 5, pp.173-182, 1974.

[15] F. Becker, and Z. L. Li, Towards a local split window method over land surface. International Journal of Remote Sensing, vol. 11, pp. 1509-1522, 1990.

[16] J. C. Price, 'Using spatial context in satellite data to infer regional scale evapotranspiration", IEEE Transactions on Geosciences and Remote Sensing vol.28, pp. 940-948, 1990.

[17] R. W. Saunders, "The determination of broad band surface albedo from AVHRR visible and nearinfrared radiances", International Journal of Remote Sensing, vol. 11, pp. 49-68, 1990.

[18] P. J. Sellers, Y. Mintz, Y. C. Sud and A. Dalcher, 1986, A simple biosphere model (SiB) for use within general circulation models. Journal of Atmospheric Science, vol.43, pp.305-331, 1986.

[19] D. Tanre, C. Deroo, P. Duhaut, J. J. Herman, J. J. Morcrette, J. Perbos and P.Y.Deschamps, Description of a computer code to simulate the satellite signal in the solar spectrum: the 5S Code", International Journal of Remote Sensing, vol. 11, pp. 659-668, 1990.

[20] C. G. Justus, M. V. Paris, and J. D. Tarpley, "Satellite-measured insolation in the United States, Mexico, and South America", Remote Sensing of Environment, vol.20,57-83,1986.

[21] W. Brutsaert, On a derivable formula for long-wave radiation from clear skies. Water Resources Research, vol. 11, pp.742-744, 1975.

[22] P. J. Sellers., J. A. Berry, G. J. Collatz, C. B. Field and F. G. Hall, "Canopy reflectance, photosynthesis and transpiration. III. A reanalysis using improved leaf models and a canopy integration scheme", Remote Sensing of Environment, vol.42, pp. 187-216, 1992.

[23] C. H. B. Priestley, and R. J. Taylor, "On the assessment of surface heat flux and evaporation using large-scale parameters", Mon. Weather Rev., vol. 100, pp.81-92,1972.